The image shooting rate to achieve a given frontal overlap depends on the speed of the UAV/plane, the GSD and the pixel resolution of the camera.

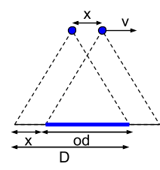
	D = distance covered on the ground by one image in the flight direction [m] overlap = percentage of desired frontal overlap between two images od = overlap between two images in the flight direction [m] x = distance between two camera positions in the flight direction [m]   v = flight speed [m/s] t = elapsed time between two images (image rate) [s]
Figure 1.

From Figure 1, we obtain the following equations:

od = overlap * D      (1)

x = D - od                (2)

t = x / v                   (3)

Two cases are possible:

• Camera oriented with the sensor width (long dimension) perpendicular to the flight direction (usual case)
• Camera oriented with the sensor width (long dimension) parallel to the flight direction

Camera oriented with the sensor width (long dimension) perpendicular to the flight direction (usual case)

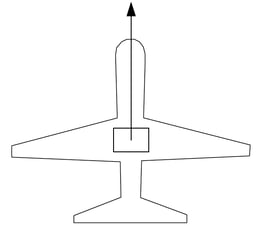
	D = Dh = (imH * GSD) / 100     (4) Where:  Dh = distance covered on the ground by one image in the height direction (footprint height) [m] imH = image height [pixel] GSD = desired GSD [cm/pixel]
Figure 2. Sensor width placed perpendicular to the flight direction.

Combining Equations (1) and (4) into Equation (2):

x = D_h - overlap * D_h

x = D_h * (1 - overlap)

x =  ((imH* GSD) / 100) * (1 - overlap)     (5)

Combining the equations (3) and (5):

t = x / v = ((imH * GSD) / 100) * (1 - overlap) / v     (6)

Camera oriented with the sensor width (long dimension) parallel to the flight direction

If the camera is placed on the plane / UAV having the sensor width (long dimension) parallel to the flight direction:

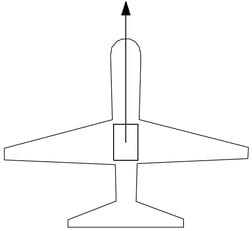
	D = DW = (imW * GSD) / 100     (7) Where:  DW = distance covered on the ground by one image in the width direction (footprint width) [m] imW = image width [pixel] GSD = desired GSD [cm/pixel]
Figure 3. Sensor width placed parallel to the flight direction.

Combining equations (1) and (7) into the equation (2):

x = D_W - overlap * D_W

x = D_W * (1 - overlap)

x =  ((imW * GSD) / 100) * (1 - overlap)     (8)

Combining equations (3) and (8):

t = x / v = ((imW * GSD) / 100) * (1 - overlap) / v     (9)